Peter West
Linear Algebra 232B
University of Puget Sound
Combinations of Subspaces
Combinations of subspaces may or may not produce new subspaces. This is useful, as it allows one to determine the dimension of a space, based upon the number of different subspaces contained within.
Consider the zero vector, a point subspace. Two orthogonal lines run through it, intersecting at the origin. These two lines, each a subspace alone, can describe a plane, a two-dimensional subspace. This plane then has another dimension added to it in the form of a third orthogonal line, and a three-dimensional space now can be described. Another line is added to this, but this line does not create a new subspace, instead being a linear combination of existing spaces. So we now know that we are dealing with a three-dimensional object, based on the combinations of existing subspaces and whether or not these combinations form new subspaces.
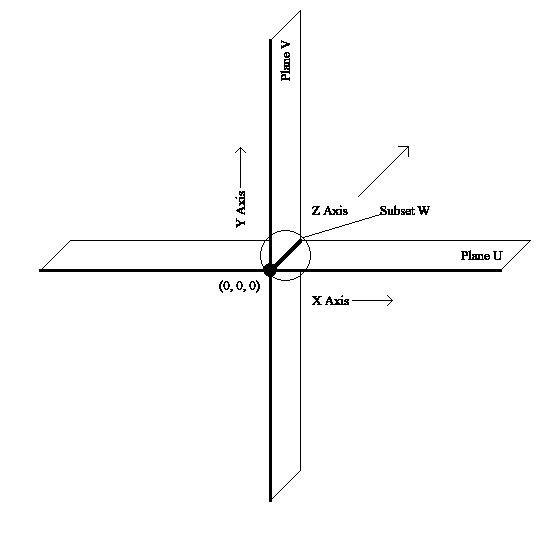
However, the way in which subspaces are combined is important, as two subspaces, meeting to form a new subset, may or may not form a new subspace, depending on how they are joined. We shall demonstrate this using two orthogonal two-dimensional planes, both of infinite area and passing through the origin, and combining them in different ways, in this case a comparison between an intersection between subspaces and a union of the same. We shall label these planes, both of which qualify as subspaces, U and V. The subset created by these planes interacting with each other is labeled subset W.
For a subset W of Rn, where Rn is the maximum dimension being worked within, to be defined as a subspace, three criteria must be met.
If even one of these tests fail, then W is not a subspace.
First, we shall create an intersection between U and V at the origin (see Figure 1). The intersection is defined as the set common between the sets said to intersect.
We wish to determine whether W is a subspace, so we shall compare the intersection against the defining criteria for a subspace.

Figure 1
1. Does W contain the zero vector?
It may or it may not, depending on the situation. As long as the intersection occurs at the origin, W does contain the zero vector. If U and V do not intersect at the origin, W will not contain this vector, and so would not qualify as a subspace. In our example however, this problem does not occur, and W meets the first criteria of a subspace.
2. Is W closed under addition?
Yes. As shown in Figure 1, W is a line identical to the Z-axis, running through the origin between positive and negative infinity. Any two vectors within W, added together, will remain on this line. Any vector composed solely of elements of W, and thus only existing on the Z-axis, added to any other vector composed of elements of W, will create a new vector along the Z-axis, which is contained within W. Therefore, any vector made up of elements of W will stay within W, making W closed under addition. W meets the second criteria of a subspace.
3. Is W closed under scalar multiplication?
Yes. Any vector within W, and therefore a vector on the Z-axis, may be multiplied by a scalar to obtain a new vector. This new vector, however, will still be described solely in terms of elements of W, the Z-axis. Therefore, W is closed under scalar multiplication.
The intersection at the origin between the subspaces U and V, subset W, meets all three criteria to qualify as a subspace of Rn.
Next, we will consider the union between U and V. The union between two sets is defined as the set of elements contained within one set, the other, or both. Does the subset W created by the union of U and V at the origin qualify as a subspace? Do determine this, we compare Figure 2 to the tests of a subspace.
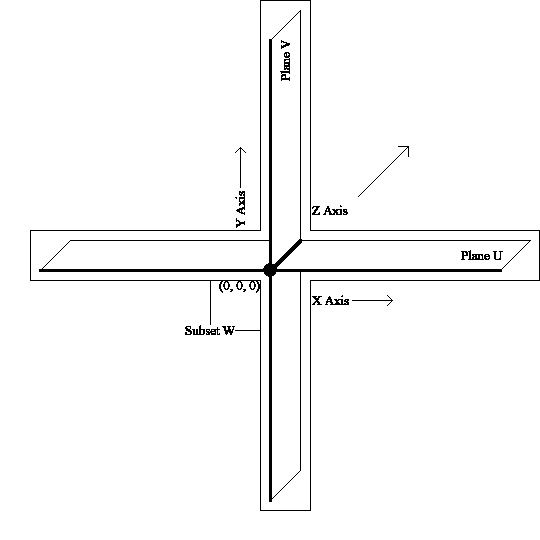
Figure 2
1. Does W contain the zero vector?
Yes. As both U and V contain the zero vector, and W is the set made up of all elements of U and V, W does contain the zero vector.
No. If, for example, we add the vector (m, 0), an element of both U and W, to the vector (0, n), an element of both V and W, we would obtain the vector (m, n). This vector may or may not be an element of W, depending upon the values of m and n. Therefore, W is not closed addition.
3. Is W closed under scalar multiplication?
Yes. If, for example, the vector (m, 0), an element of both U and W, was multiplied by the scalar k, the new vector would be (km, 0). As k is a constant scalar and m is contained within the infinitely large area of W, km would be contained within W, regardless of the actual values of either k or m. Therefore, W is closed under scalar multiplication.
The union at the origin between U and V at the origin, subset W, fails the second criteria necessary to qualify as a subspace of Rn.
Combinations of subspaces can easily be tested to see if the combination can create a new subspace. By examination of these subspaces, one can determine the dimension of a space based upon the number of types of subspaces it contains.